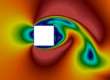
Turbulent flow in a 90° bend
The flows in pipe (straight, bent …) are involved in many industrial processes such as heat exchangers and cooling systems, piping etc. Experimentally this type of flow was largely studied in the 1980s in rectangular pipe (pressure loss measurements, velocity fields with Pitot tube …). In 1998 Sudo et al [1] carried out a study on the turbulent flow in a 90 ° elbow of cylindrical section. For this article we will try to compare the experimental results of Sudo with those obtained with the simpleFoam solver of OpenFOAM®. This article aims to illustrate the possibilities of open-source tools for all stages of the modeling process, namely:
- Salome for the creation of the 3D model of the elbow
- BlockMesh and SnappyHexMesh for hexahedral and cartesian mesh
- OpenFOAM® for the resolution of the numerical model (turbulent incompressible solver in steady-state: simpleFoam)
- Paraview and Python for post-processing
Experimentally, Sudo et al measured the vertical and horizontal distribution of the velocity field (longitudinal component) at different positions of the flow (upstream of the elbow, at the elbow and downstream of the elbow). Measurements were obtained using a hot-wire anemometer. It should be noted that the Reynolds stress distribution has also been measured.
References
[1] : K. Sudo, M. Sumida, H. Hibara – Experimental investigation on turbulent flow in a circular-sectioned 90-degree bend. Experiments in Fluids 25 (1998) 42—49 ( Springer-Verlag 1998 )
paper link : https://link.springer.com/article/10.1007/s003480050206.
Geometry
The diameter of the pipe studied is d = 104 mm. The curvature radius of the elbow is Rc = 208 mm (2d). Experimentally the lengths of the straight sections upstream and downstream of the elbow are respectively 100d and 40d. The line is supplied with air (temperature and atmospheric pressure) at 8.7 m/s (Reynolds number 60000). The 3D model is made under Salome and exported in stl format. The upstream and downstream portions of the elbow are limited to 50d and 20d (which is sufficient here to obtain a fully developed flow).
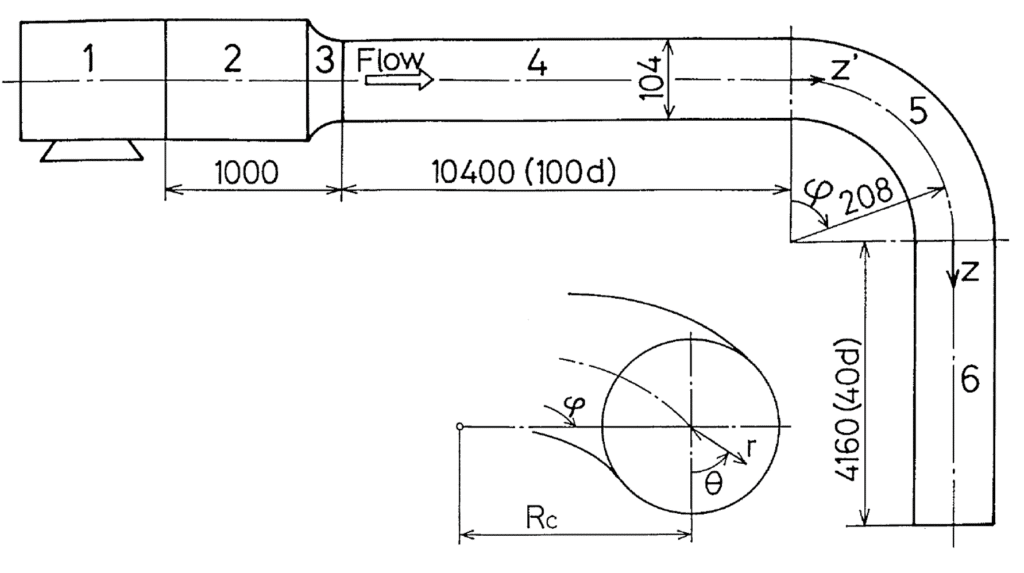
Figure 1 : Experimental device (Sudo et al 1998), (left) – Salome stl surface (center and right)
Mesh
The mesh of level 0 or background mesh (generated with blockMesh) is used to intersect the surface (.stl) of the pipe respectively at the the median plane, the entry plane and exit thus generating the patches of symmetry, input and output of the computational domain.
The mesh of the pipe is generated with snappyHexMesh starting from the “background” mesh. Boundary layer elements are inserted in the near wall region to capture the parietal gradients. The average value of the y+ obtained is 30 (first element located in the log area). In addition, the snappyHexMesh distance mode is used to refine the cells according to the distance to a given patch (here, the wall), which makes it possible to significantly improve the insertion of the boundary layer elements. Finally a refinement block is defined at the elbow region.
The total number cells is 1.1M. No error is detected by the checkMesh utility.
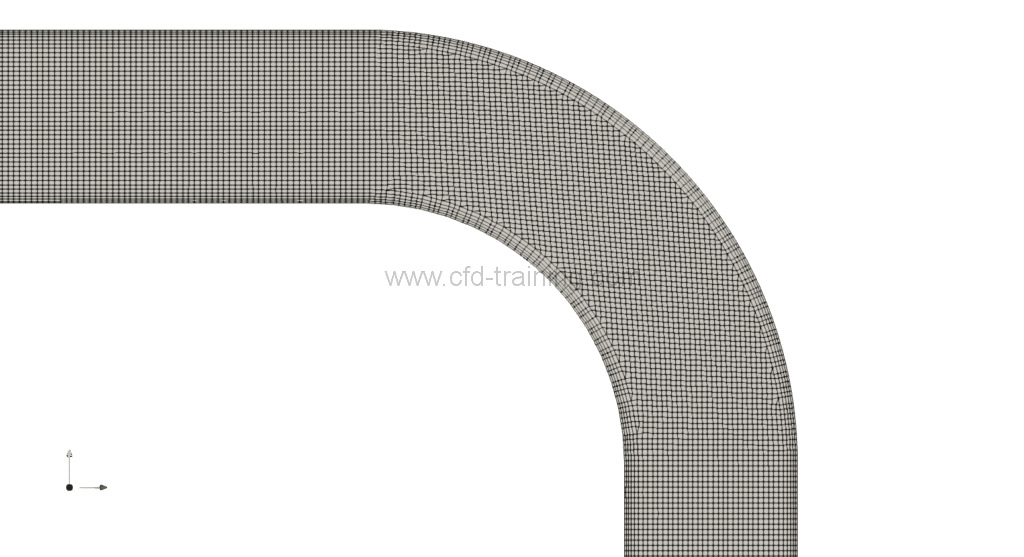
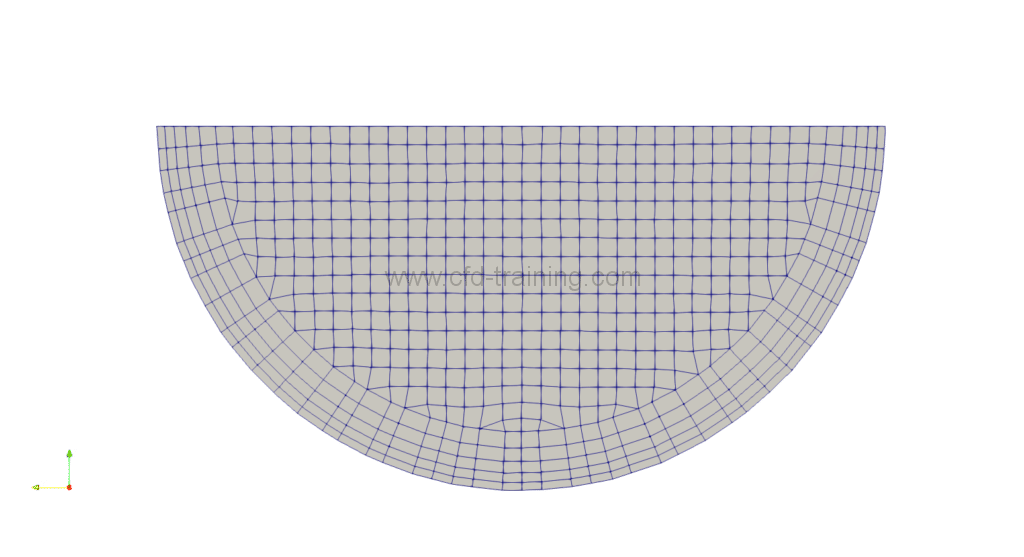
Figure 2 : Cartesian mesh – Mean y+ ~ 30
Boundary conditions
The following table resumes the boundary condition used for the numerical model:
| U | k | epsilon | p | nut | |
|---|---|---|---|---|---|
| Inlet patch | fixedValue (8.7 m/s) | fixedValue | fixedValue | zeroGradient | calculated |
| Outlet pach | zeroGradient | zeroGradient | zeroGradient | fixedValue 0 | calculated |
| Wall patch | noSlip | kqRWallFunction | epsilonWallFunction | zeroGradient | nutkWallFunction |
| Symmetry patch | symmetry | symmetry | symmetry | symmetry | symmetry |
Note that the kqRWallFunction boundary condition is equivalent to a zeroGradient condition.
For k and epsilon assessment the reader is invited to read the Turbulent boundary conditions calculator.
Numerical settings
Schemes
Centered difference is used for gradient and divergence (linear keyword under OpenFOAM®). The Laplacian operator is also discretized with a centered difference type scheme.
[pastacode lang=”cpp” manual=”ddtSchemes%0A%7B%0A%20%20%20%20default%20%20%20%20%20%20%20%20%20steadyState%3B%0A%7D%0A%0AgradSchemes%0A%7B%0A%20%20%20%20%20%20default%20%20%20%20%20%20%20Gauss%20linear%3B%0A%7D%0A%0AdivSchemes%0A%7B%0A%20%20%20%20default%20%20%20%20%20%20%20%20%20Gauss%20linear%3B%0A%20%20%20%20div((nuEff*dev2(T(grad(U)))))%20Gauss%20linear%3B%0A%7D%0A%0AlaplacianSchemes%0A%7B%0A%20%20%20%20default%20%20%20%20%20%20%20%20%20Gauss%20linear%20corrected%3B%0A%7D%0A%0AinterpolationSchemes%0A%7B%0A%20%20%20%20default%20%20%20%20%20%20%20%20%20linear%3B%0A%7D%0A%0AsnGradSchemes%0A%7B%0A%20%20%20%20default%20%20%20%20%20%20%20%20%20corrected%3B%0A%7D” message=”” highlight=”” provider=”manual”/]
Pressure velocity coupling
The solver used is the simpleFoam solver (incompressible monophasic flow) based on the SIMPLE loop (Semi-Implicit Method for Pressure-Linked Equations). For the presented study, the consistent option is enabled to use the SIMPLEC loop. The SIMPLEC loop has the advantage over the standard SIMPLE loop of being more robust and faster. The numerical model being robust due to the mesh quality non-orthogonal corrector are not necessary. In addition, to facilitate the simpleFoam convergence relaxation factors are introduced.
[pastacode lang=”cpp” manual=”SIMPLE%0A%7B%0A%20%20%20%20nNonOrthogonalCorrectors%200%3B%0A%20%20%20%20consistent%20yes%3B%0A%7D%0A%0ArelaxationFactors%0A%7B%0A%20%20%20%20equations%0A%20%20%20%20%7B%0A%20%20%20%20%20%20%20%20U%20%20%20%20%20%20%20%20%20%20%20%20%20%20%200.7%3B%0A%20%20%20%20%20%20%20%20k%20%20%20%20%20%20%20%20%20%20%20%20%20%20%200.5%3B%0A%20%20%20%20%20%20%20%20epsilon%20%20%20%20%20%20%20%20%200.5%3B%0A%20%20%20%20%20%20%20%20p%20%20%20%20%20%20%20%20%20%20%20%20%20%20%200.5%3B%0A%20%20%20%20%7D%0A%7D” message=”SIMPLE(C) settings” highlight=”” provider=”manual”/]
Linear solvers
- The resolution of the velocity equation uses the smoothSolver with symGaussSeidel smoother .
- The resolution of the pressure equation uses the GAMG solver (geometric-algebraic multi-grid) with a DIC (diagonal incomplete-Cholesky) preconditioner.
Results
The figures below show the calculation results obtained with simpleFoam:
Velocity field
Figure 3 : Velocity field (m/s) cut plane
Horizontal and vertical velocity distribution
The horizontal velocity profiles are located in the model symmetry plane while the vertical profiles are perpendicular to the symmetry plane and located at pipe center. The profiles are marked from the distances z ‘and z and the angle phi shown in Figure 1.
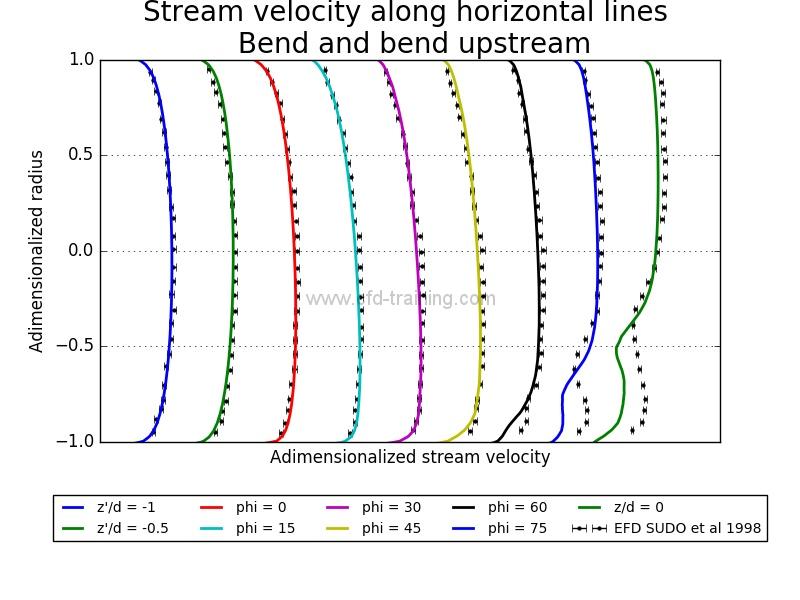
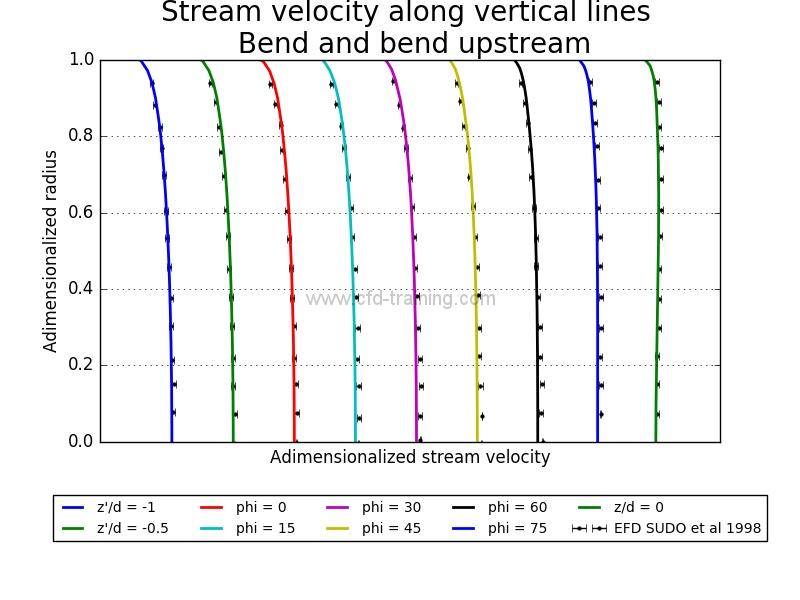
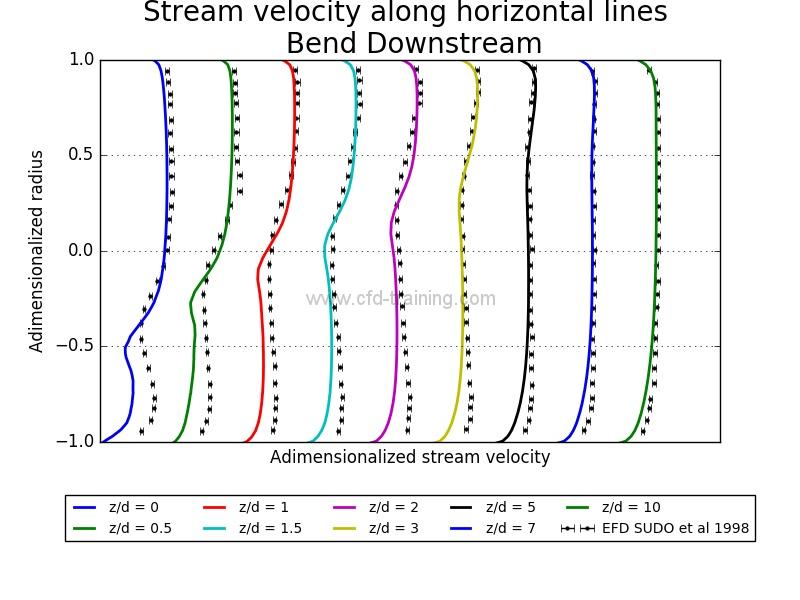
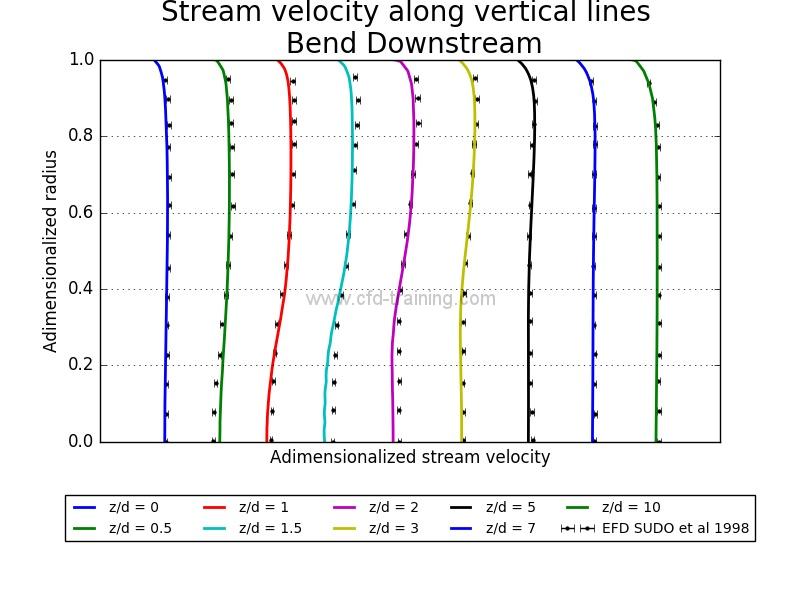
Figure 4 : Numerical/Experimental comparison of spatial mean velocity distribution
Conclusions
This post illustrated, how to set up the numerical model of turbulent flow in a 90 ° elbow using opensource tools. The simpleFoam solver from OpenFOAM® was used and the comparison of the results with the Sudo et al measurements is rather encouraging. In terms of vertical velocity distributions the differences are relatively small. Regarding horizontal distributions, some differences remain at the level of the elbow in the internal region. They are probably due to turbulence anisotropies not taken into account by the standard model k-epsilon. The study should be completed using other turbulence models.
